1. Задание № 114 
Сложность: III
Классификатор алгебры: 6\.2\. Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Замена переменной
Методы тригонометрии: Формулы кратных углов
Тригонометрические уравнения
i
Найдите количество корней уравнения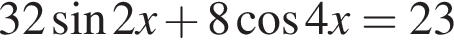 
на промежутке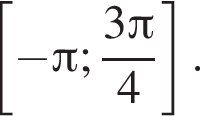 
Решение. Решим уравнение:
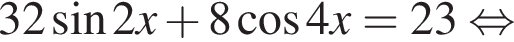
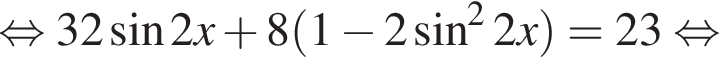
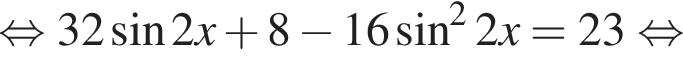
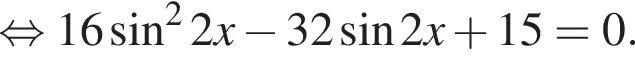
Сделаем замену: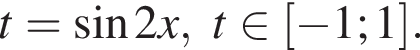 
Тогда:
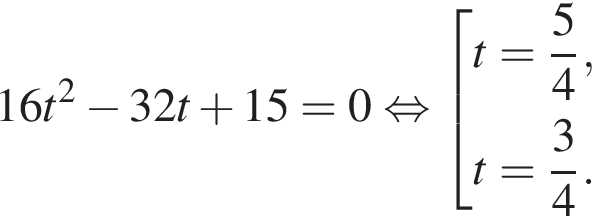
Первый корень не удовлетворяет условию замены, следовательно,
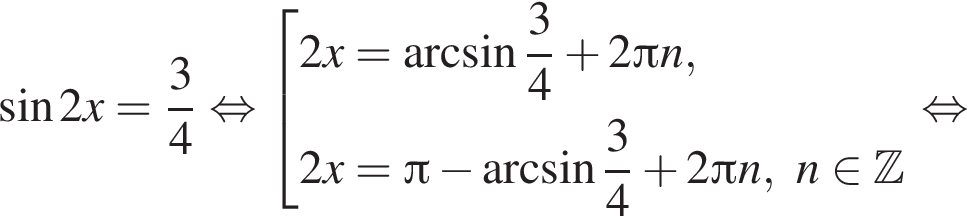
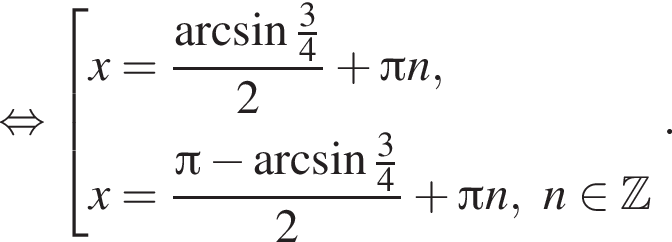
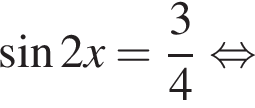
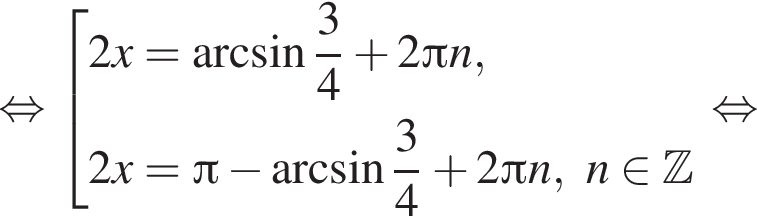
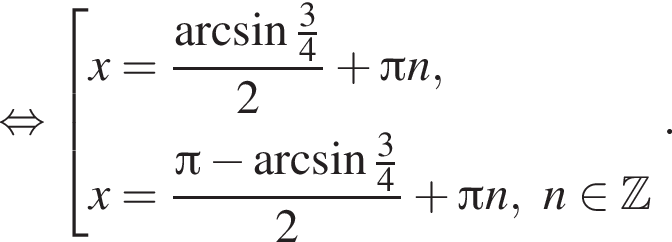
Отметим, что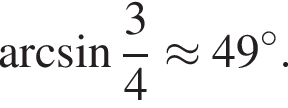 
Рассмотрим значения x при различных значениях n:
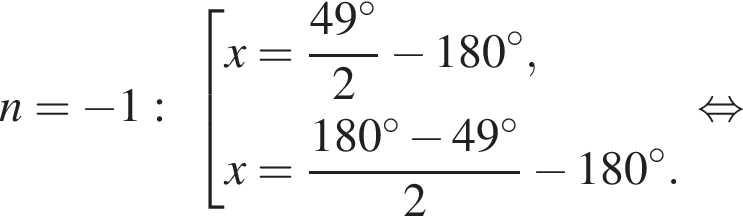
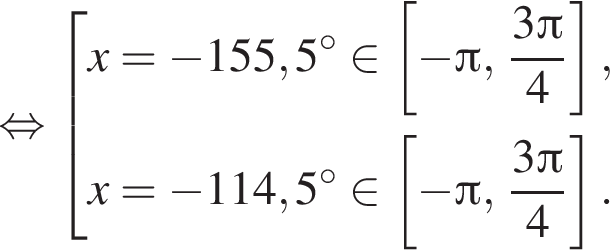
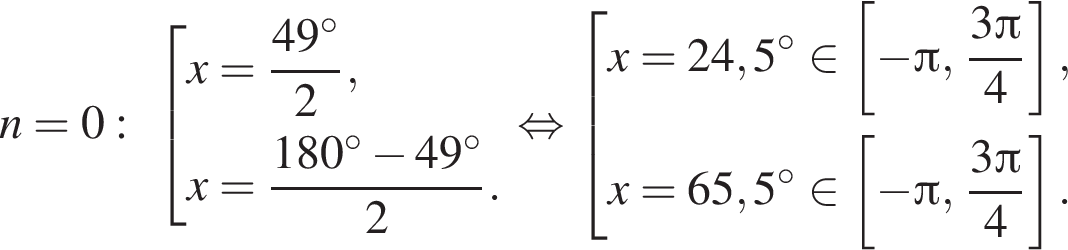
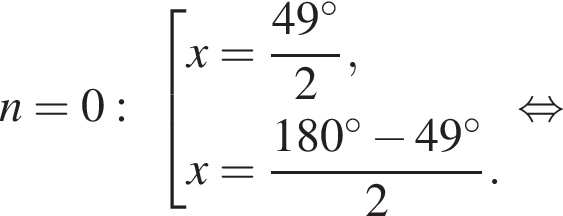
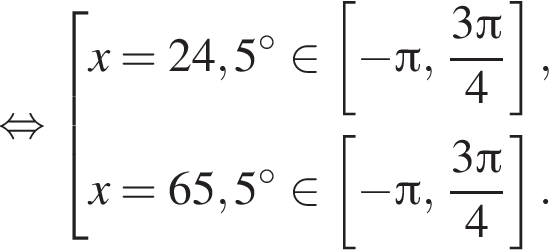
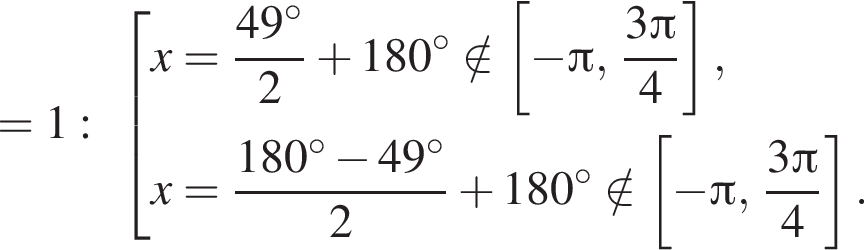
Таким образом, на промежутке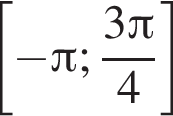 
4 корня.
Ответ: 4.
Ответ: 4
114
4
Сложность: III
Классификатор алгебры: 6\.2\. Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Замена переменной
Методы тригонометрии: Формулы кратных углов
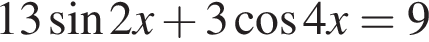на промежутке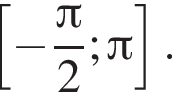 
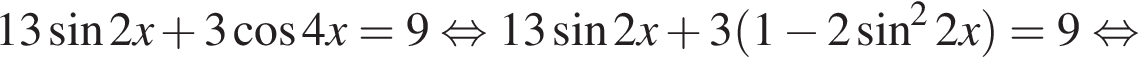
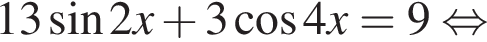
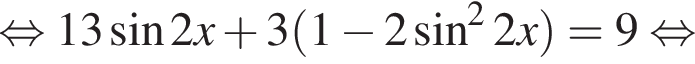
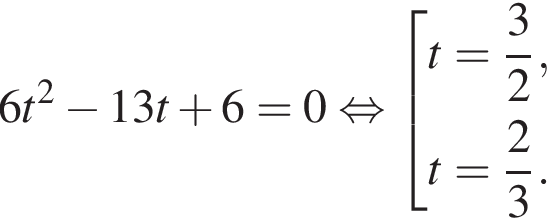
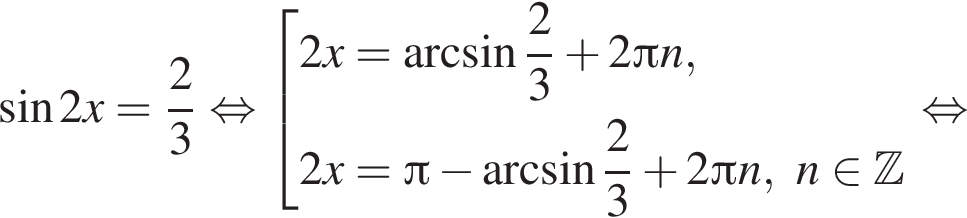
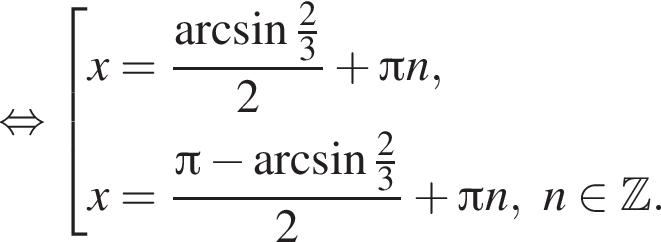
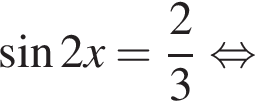
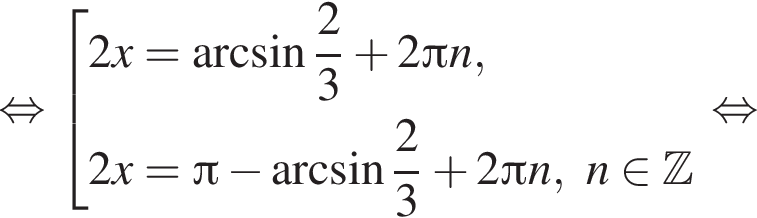
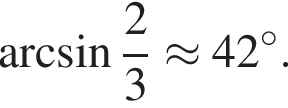Рассмотрим значения x при различных значениях n: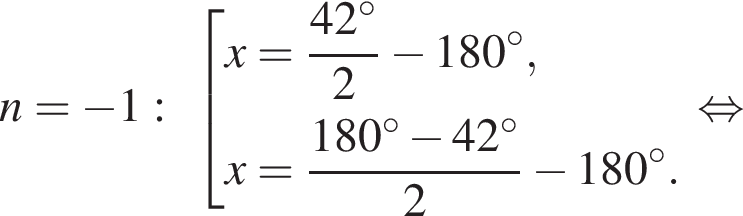
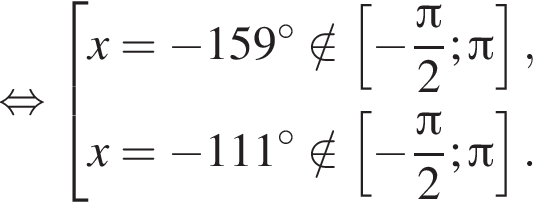
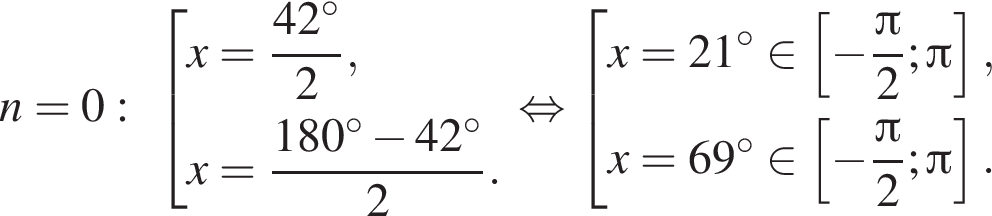
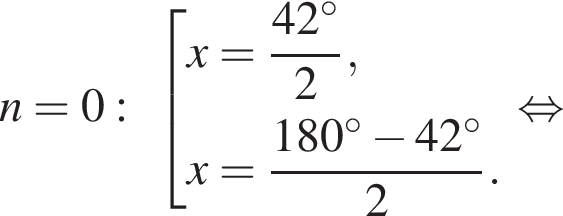
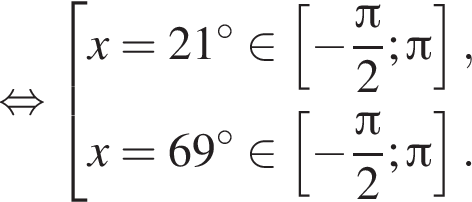
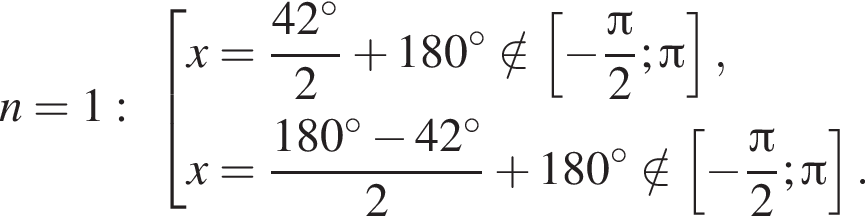
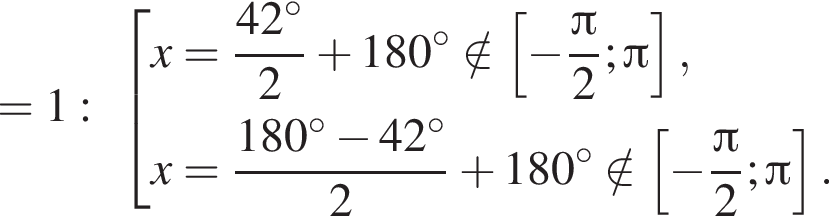
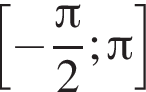2 корня.
на промежутке 
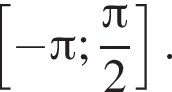
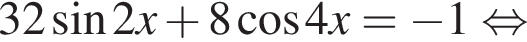
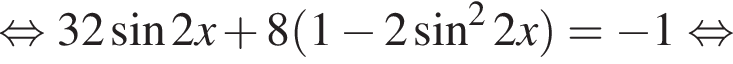
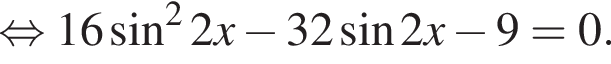
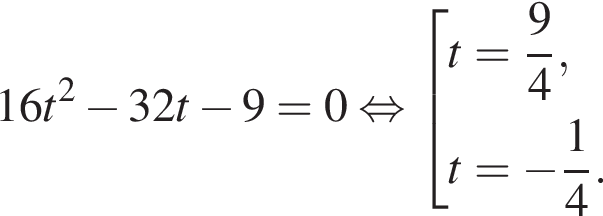
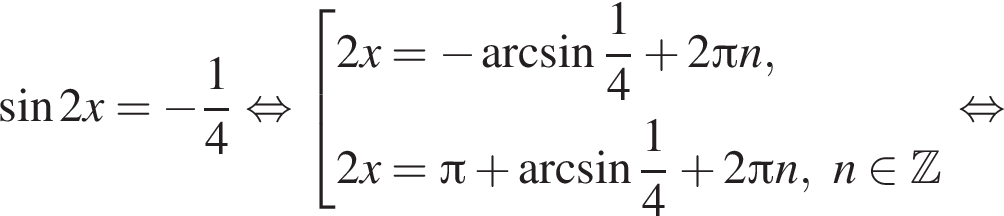
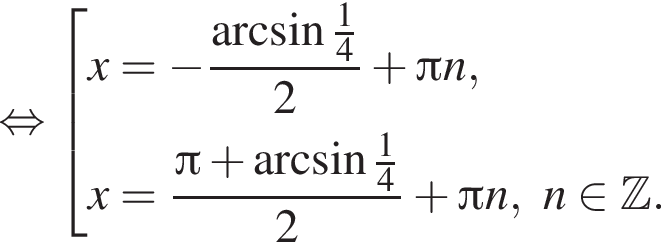
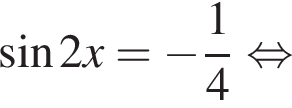
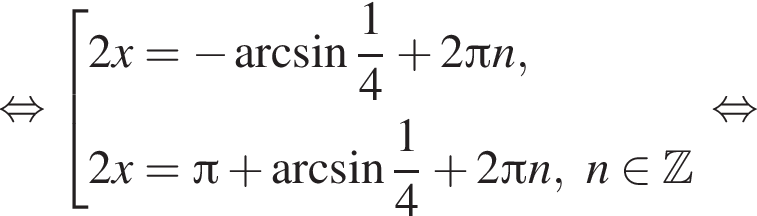
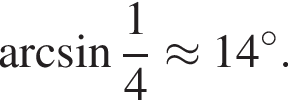Рассмотрим значения x при различных значениях n: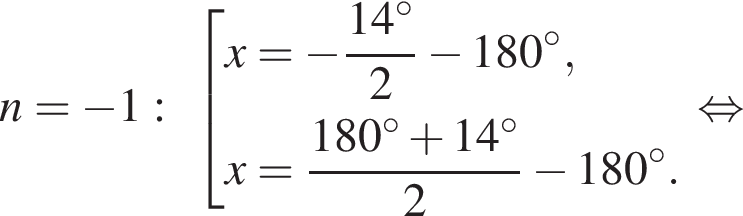
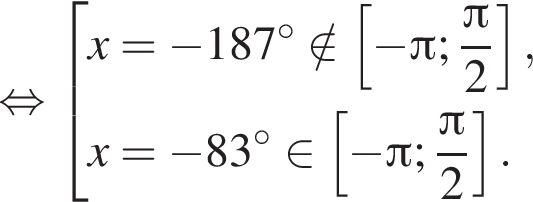
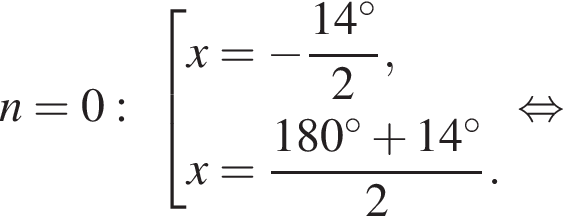
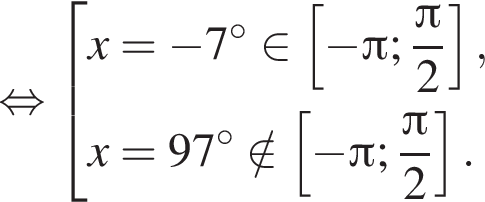
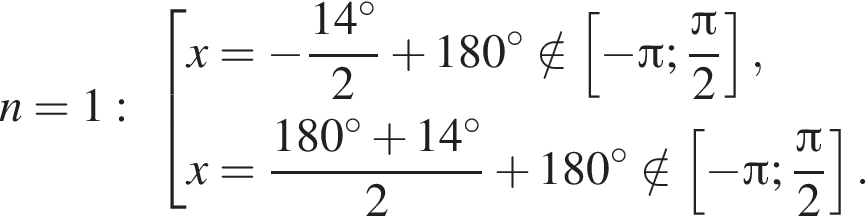
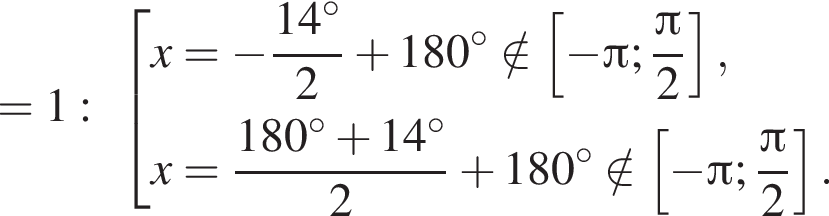
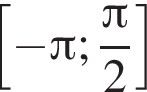2 корня.
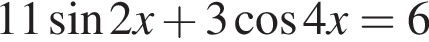на промежутке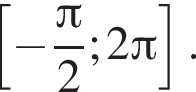 
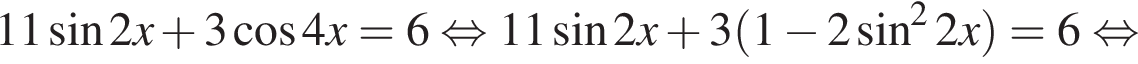
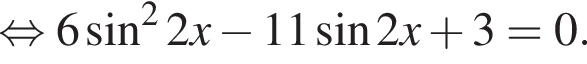
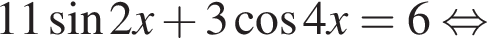
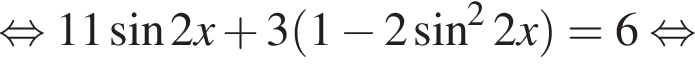
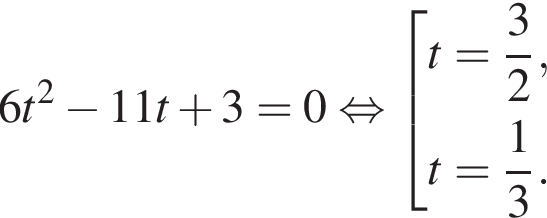
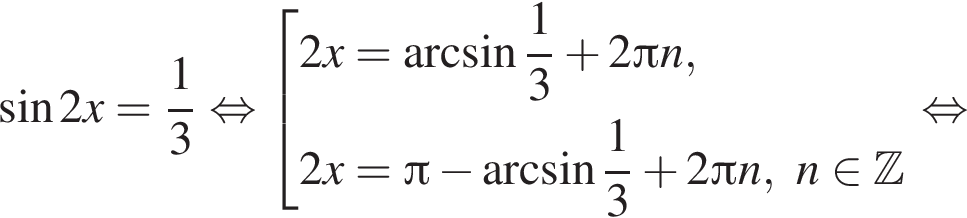
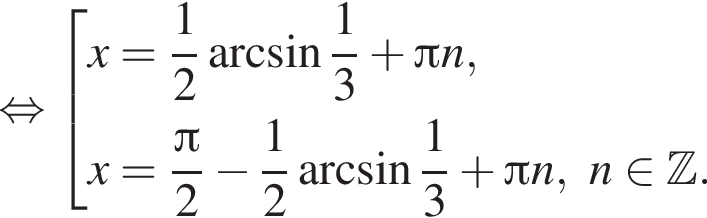
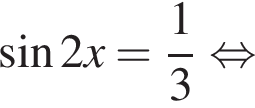
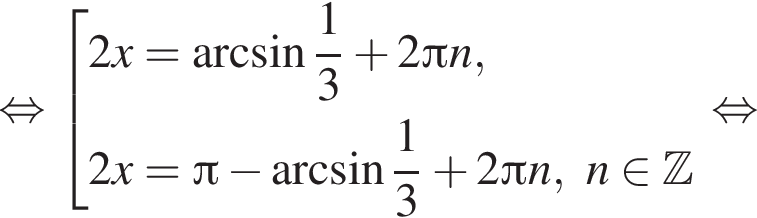
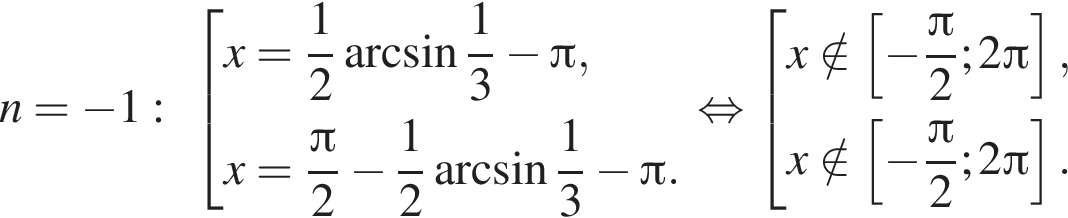
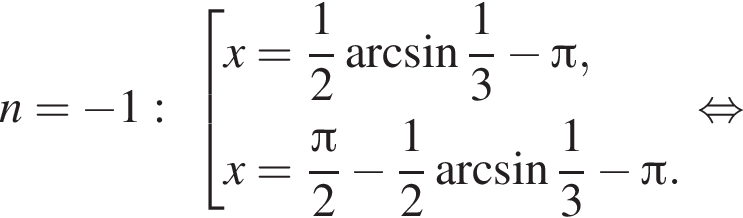
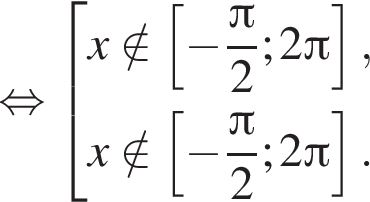
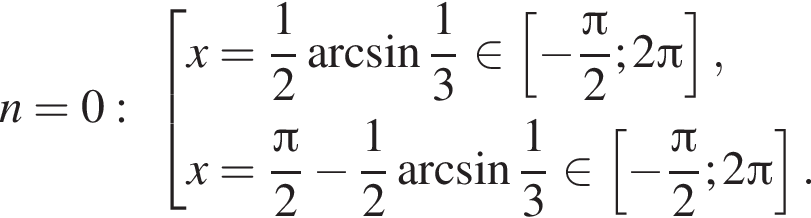
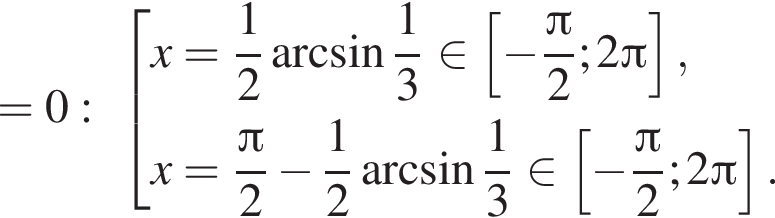
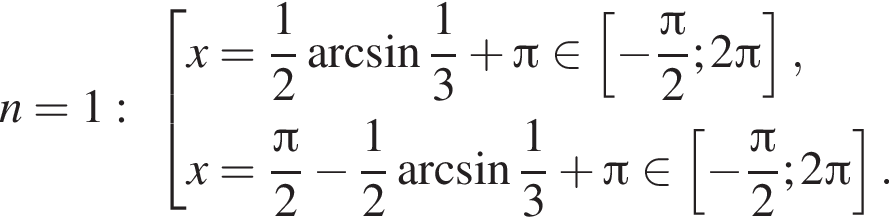
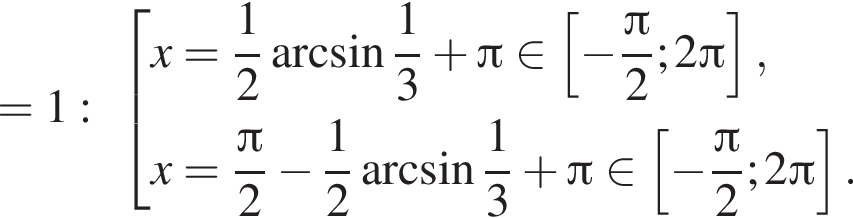
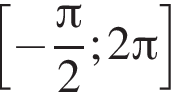4 корня.
на промежутке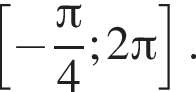 
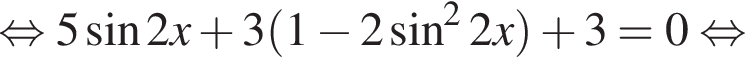
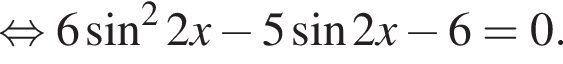
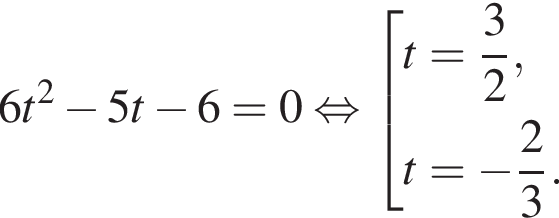
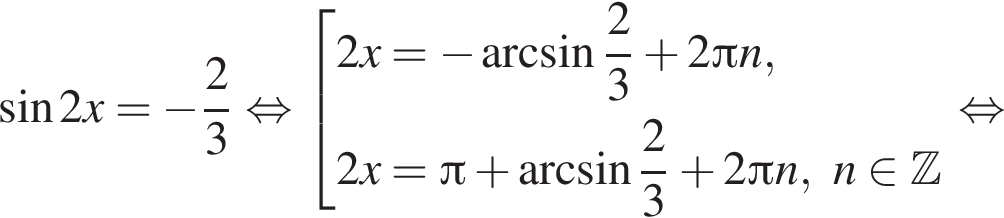
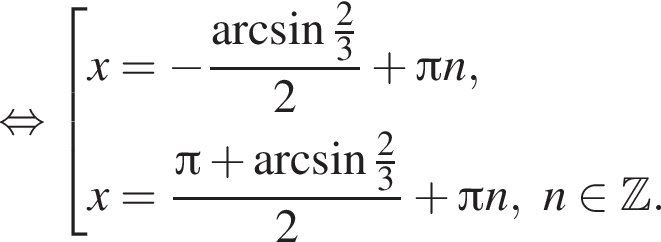
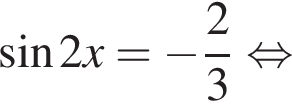
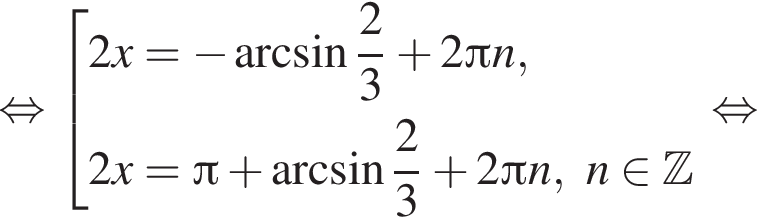
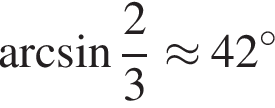. Рассмотрим значения x при различных значениях n: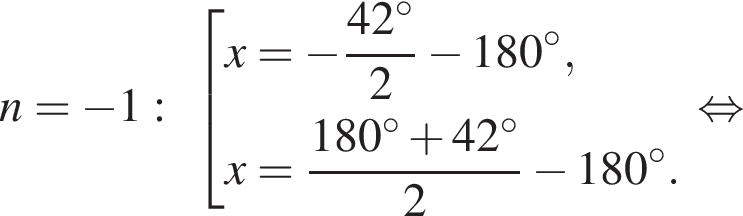
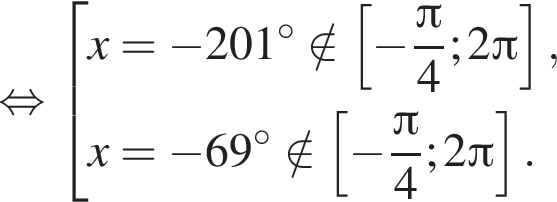
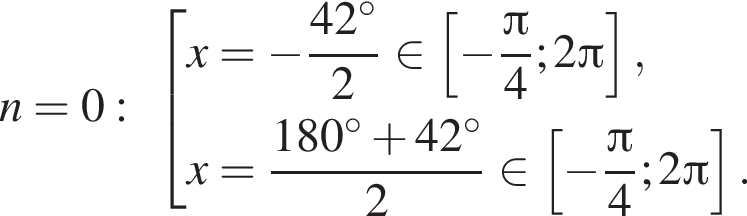
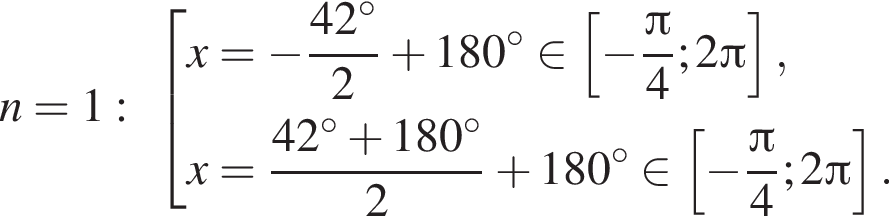
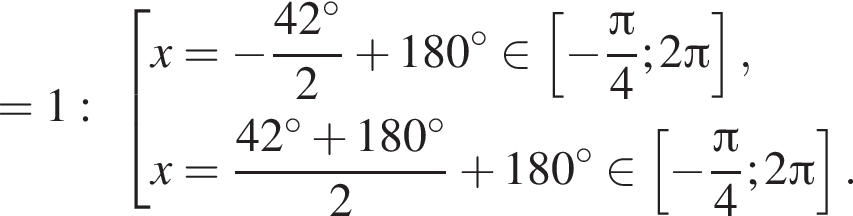
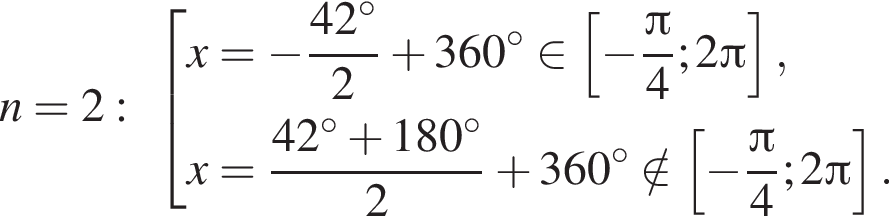
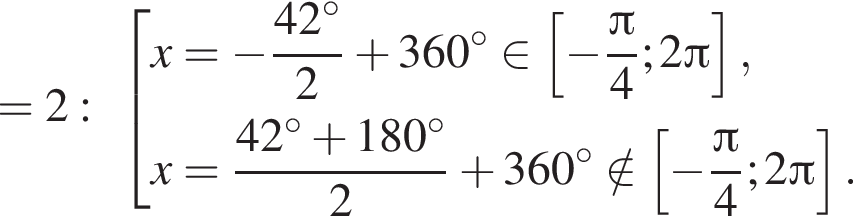
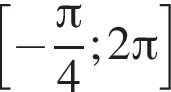5 корней.